現代セキュリティの基盤となっている公開鍵暗号の処理には、通常コンピュータのマシン命令では直接取り扱えないような大きな整数の演算を高い性能で実現する必要があります。wolfSSLではそのために、開発の当初から独自に専用の数学(整数)ライブラリを開発、使用しています。現在、その第三世代というべき整数ライブラリ(SP-math:Single Precision Math)が活躍しています。この記事では、この発展を簡単に振り返りSPによる数学ライブラリの特徴と使い方についてまとめます。
第一世代として開発された整数ライブラリは特別の名前を持っていませんが、現在は他のライブラリと区別するためにノーマル数学(Normal Math)ライブラリなどと呼んでいます。wolfSSLでは最近まで強化、改善を続けてきたのですが、サイドチャネル攻撃のリスクを回避することが難しいなどの理由で今年末までに削除する方向です。
第二世代は、パブリックドメインのTFM(Tom’s Fast Math)をベースにwolfSSLで独自に強化、改善を続けてきたライブラリです。第一世代にくらべて、性能的に強化されていると同時に上記のようなセキュリティリスクへの対策もとられています。
第三世代は、SP(Single Precision)最適化とよばれる特定の鍵サイズに着目した最適化手法をベースとしています。SPではさらにSIMD命令のような並列処理向けのアーキテクチャ固有の機能を使い最大の性能を実現しています。
現バージョンのSP最適化は、256, 384, 512, 521ビットのECC, 2048, 3072, 4096ビットのRSA鍵に対応しているので、ほとんどの場合この最適化の恩恵をうけることができますが、wolfSSLのデフォルトのコンフィグレーションではTFMをベースとした可変鍵長を扱うことのできるMP(Multiple Precision) とのハイブリッド型の処理を行うようになっています。実行時には、処理対象の鍵サイズによってSP最適化の対象サイズであればSPで処理し、対象外であればTFMで処理します。これによって、ユーザはSPの対象かどうかを意識することなく、鍵サイズに応じて最適な処理を選択することができます。
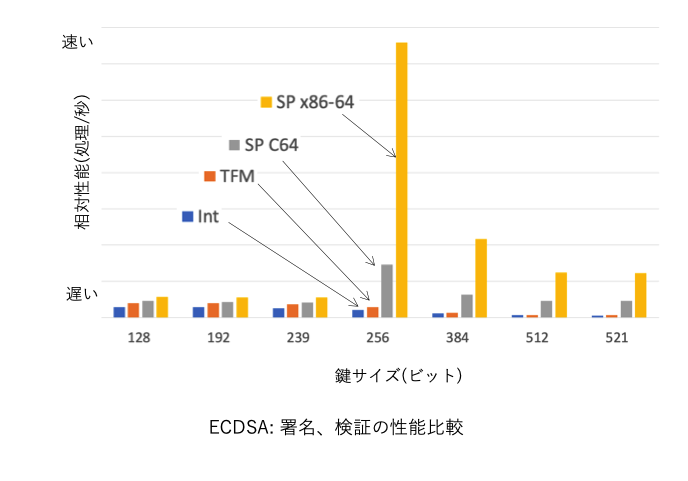
下のグラフにECC暗号処理性能の例として、ECDSA署名生成と検証の性能を各鍵サイズで比較します。ここでは、第一世代のノーマル整数、第二世代のTFMと第三世代のSP(ハイブリッド型)を比較しています。SPはさらに、鍵サイズ固定であることを活かした掛け算回数の削減などC言語レベルでの最適化のみを行ったもの(C64)場合と、プロセッサアーキテクチャ向け最適化まで行った場合(このグラフではx85-64)があり、これらを比較しています。縦軸は、毎秒の処理回数を相対値で表しているので、縦棒が長いほうが処理速度が速いことを表します。グラフからわかるように、SP最適化の対象となっている鍵サイズではきわめて大きな性能改善が実現されていることがわかります。
デフォルトのハイブリッド型ではコードサイズがやや大きくなってしまうので、組込みシステムなどコードサイズの制限が強いシステム向けにはやや注意する必要があります。あらかじめ処理対象の鍵サイズがわかっている場合はコンフィグレーションオプションの指定で、SP最適化だけを単独で利用することが可能です。また、特定の鍵サイズの処理ロジックだけを切り出し、使用しない鍵サイズのためのコードを削減することもできます。
SP最適化では、ヒープとスタックのメモリ使用量についても最小となるように改善されています。特にヒープメモリについては、例えば署名の検証のようにいくつかの処理においては使用しないで処理を実現しています。
wolfSSLの数学ライブラリについてさらに詳しい情報をご希望のかたは、info@wolfssl.jp 宛お問い合わせください。
